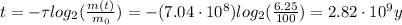Question

Analysis of a rock sample shows that it contains 6.25% of its original uranium-235. How old is the rock? How do you know?

Answer 1

`2.82\cdot 10^9 y`

Step-by-step explanation:

A radioactive isotope is an isotope that undergoes nuclear decay, breaking apart into a smaller nucleus and emitting radiation during the process.

The half-life of an isotope is the amount of time it takes for a certain quantity of a radioactive isotope to halve.

For a radioactive isotope, the amount of substance left after a certain time t is:

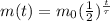`m(t)=m_0 ((1)/(2))^{(t)/(\tau)}` (1)

where

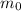`m_0` is the mass of the substance at time t = 0

m(t) is the mass of the substance at time t

`\tau` is the half-life of the isotope

In this problem, the isotope is uranium-235, which has a half-life of

`\tau=7.04\cdot 10^8 y`

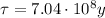
We also know that the amount of uranium left in the rock sample is 6.25% of its original value, this means that

`(m(t))/(m_0)=(6.25)/(100)`

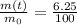
Substituting into (1) and solving for t, we can find how much time has passed:

`t=-\tau log_2 ((m(t))/(m_0))=-(7.04\cdot 10^8) log_2 ((6.25)/(100))=2.82\cdot 10^9 y`