Question

Suppose the number of children in a household has a binomial distribution with parameters n=12n=12 and p=50p=50%. Find the probability of a household having: (a) 2 or 5 children (b) 3 or fewer children (c) 8 or more children (d) fewer than 5 children (e) more than 3 children

Answer 1

a) 20.95% probability of a household having 2 or 5 children.

b) 7.29% probability of a household having 3 or fewer children.

c) 19.37% probability of a household having 8 or more children.

d) 19.37% probability of a household having fewer than 5 children.

e) 92.71% probability of a household having more than 3 children.

Explanation:

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

In this problem, we have that:

`n = 12, p = 0.5`

(a) 2 or 5 children

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(12,2).(0.5)^(2).(0.5)^(10) = 0.0161`

`P(X = 5) = C_(12,5).(0.5)^(5).(0.5)^(7) = 0.1934`

`p = P(X = 2) + P(X = 5) = 0.0161 + 0.1934 = 0.2095`

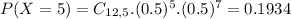
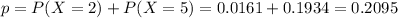
20.95% probability of a household having 2 or 5 children.

(b) 3 or fewer children

`P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(12,0).(0.5)^(0).(0.5)^(12) = 0.0002`

`P(X = 1) = C_(12,1).(0.5)^(1).(0.5)^(11) = 0.0029`

`P(X = 2) = C_(12,2).(0.5)^(2).(0.5)^(10) = 0.0161`

`P(X = 3) = C_(12,3).(0.5)^(3).(0.5)^(9) = 0.0537`

`P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 0.0002 + 0.0029 + 0.0161 + 0.0537 = 0.0729`

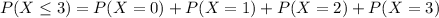
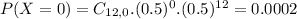
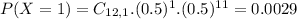
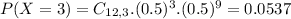
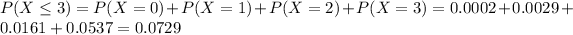
7.29% probability of a household having 3 or fewer children.

(c) 8 or more children

`P(X \geq 8) = P(X = 8) + P(X = 9) + P(X = 10) + P(X = 11) + P(X = 12)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 8) = C_(12,8).(0.5)^(8).(0.5)^(4) = 0.1208`

`P(X = 9) = C_(12,9).(0.5)^(9).(0.5)^(3) = 0.0537`

`P(X = 10) = C_(12,10).(0.5)^(10).(0.5)^(2) = 0.0161`

`P(X = 11) = C_(12,11).(0.5)^(11).(0.5)^(1) = 0.0029`

`P(X = 12) = C_(12,12).(0.5)^(12).(0.5)^(0) = 0.0002`

`P(X \geq 8) = P(X = 8) + P(X = 9) + P(X = 10) + P(X = 11) + P(X = 12) = 0.1208 + 0.0537 + 0.0161 + 0.0029 + 0.0002 = 0.1937`

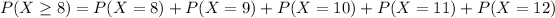
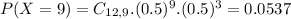
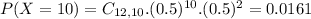
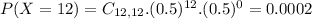
19.37% probability of a household having 8 or more children.

(d) fewer than 5 children

`P(X < 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(12,0).(0.5)^(0).(0.5)^(12) = 0.0002`

`P(X = 1) = C_(12,1).(0.5)^(1).(0.5)^(11) = 0.0029`

`P(X = 2) = C_(12,2).(0.5)^(2).(0.5)^(10) = 0.0161`

`P(X = 3) = C_(12,3).(0.5)^(3).(0.5)^(9) = 0.0537`

`P(X = 4) = C_(12,4).(0.5)^(4).(0.5)^(8) = 0.1208`

`P(X < 5) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = 0.0002 + 0.0029 + 0.0161 + 0.0537 + 0.1208 = 0.1937`

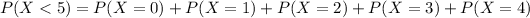
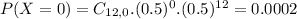
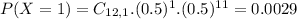
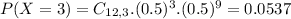
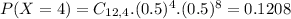
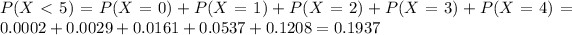
19.37% probability of a household having fewer than 5 children.

(e) more than 3 children

Either a household has 3 or fewer children, or it has more than 3. The sum of these probabilities is 100%.

From b)

7.29% probability of a household having 3 or fewer children.

p + 7.29 = 100

p = 92.71

92.71% probability of a household having more than 3 children.