Question

A 3.0-L gas mixture contains 30.% oxygen and 70.% nitrogen. Use the ideal gas law to determine the number of moles of oxygen at 2.0 atm and 400-K.

Answer 1

The number of moles of oxygen gas comes out to be 0.0548 mole

Step-by-step explanation:

Given volume of gas = V = 3.0 L

The mixture contains 30 % oxygen gas by mole.

Pressure of mixture of gas = P = 2.0 atm

Temperature = T = 400 K

Assuming n be the total number of moles of the mixture of gas.

The ideal gas equation is shown below

`\textrm{PV} = \textrm{nRT} \\2.0 \textrm{ atm}* 3.0\textrm{ L} = n * 0.0821 \textrm{ L.atm.mol}^(-1).K^(-1) * 400 \textrm{ K} \\n = 0.18270 \textrm{ mole}`

The mixture contains 30% oxygen gas by mole

`\textrm{ Number of moles of oxygen gas} = \displaystyle \frac{30* 0.18270 \textrm{ mole}}{100} = 0.0548 \textrm{ mole}`

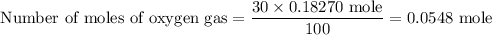
Number of moles of oxygen gas is 0.0548 mole