Question

A mass weighing 32 pounds stretches a spring 2 feet. Determine the amplitude and period of motion if the mass is initially released from a point 1 foot above the equilibrium position with an upward velocity of 6 ft/s.

Answer 1

A mass weighing 32 pounds stretches a spring 2 feet.

(a) Determine the amplitude and period of motion if the mass is initially released from a point 1 foot above the equilibrium position with an upward velocity of 6 ft/s.

(b) How many complete cycles will the mass have completed at the end of 4 seconds?

Answer:

`A = 1.803 ft`

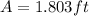
Period =
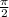`(\pi)/(2)` seconds

8 cycles

Step-by-step explanation:

A mass weighing 32 pounds stretches a spring 2 feet;

it implies that the mass (m) =
`(w)/(g)`

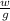
m=
`(32)/(32)`

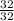
= 1 slug

Also from Hooke's Law

2 k = 32

k =
`(32)/(2)`

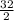
k = 16 lb/ft

Using the function:

`(d^2x)/(dt) = - 16x\\(d^2x)/(dt) + 16x =0`

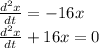
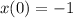`x(0) = -1` (because of the initial position being above the equilibrium position)

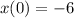`x(0) = -6` ( as a result of upward velocity)

NOW, we have:

`x(t)=c_1cos4t+c_2sin4t\\x^(')(t) = 4(-c_1sin4t+c_2cos4t)`

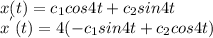
However;

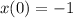`x(0) = -1` means

`-1 =c_1\\c_1 = -1`

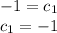
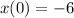`x(0) =-6` also implies that:

`-6 =4(c_2)\\c_2 = - (6)/(4)`

`c_2 = -(3)/(2)`

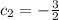
Hence,
`x(t) =-cos4t-(3)/(2) sin 4t`

`A = √(C_1^2+C_2^2)`

`A = \sqrt{(-1)^2+((3)/(2))^2 }`

`A=\sqrt{(13)/(4) }`

`A= (1)/(2)√(13)`

`A = 1.803 ft`

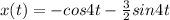
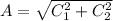
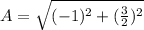
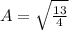
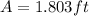
Period can be calculated as follows:

=
`(2 \pi)/(4)`

=
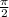`(\pi)/(2)` seconds

How many complete cycles will the mass have completed at the end of 4 seconds?

At the end of 4 seconds, we have:

`x* (\pi)/(2) = 4 \pi`

`x \pi = 8 \pi`

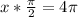
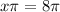
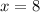`x=8` cycles