Question

The temperature T in a metal ball is inversely proportional to the distance from the center of the ball, which we take to be the origin. The temperature at the point (1, 2, 2) is 160°. (a) Find the rate of change of T at (1, 2, 2) in the direction toward the point (4, 1, 3). Incorrect: Your answer is incorrect. (b) Show that at any point in the ball the direction of greatest increase in temperature is given by a vector that

Answer 1

The answers to the questions are as follows;

(a) The rate of change of T at (1, 2, 2) in the direction toward the point (4, 1, 3) is
`(160√(11) )/(33)`

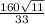
(b) The direction of the gradient is in the direction of greatest increase and it is towards the origin.

Step-by-step explanation:

To solve the question, we note that the shape of the ball is that of a sphere.

Therefore the distance of a point from the center is given by

f(x, y, z) =
`√(x^2+y^2+z^2)`

The temperature T in a metal ball is inversely proportional to the distance from the center of the ball

Therefore T ∝
`(1)/(√(x^2+y^2+z^2))` or T =
`(C)/(√(x^2+y^2+z^2))`

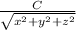
Where

C = Constant of proportionality

x, y, and z are the x, y and z coordinates values

To find C, we note that at point (1, 2, 2), T = 160 °C.

Therefore 160 °C =
`(C)/(√(1^2+2^2+2^2))` =
`(C)/(√(9))` =
`(C)/(3)}`

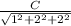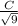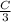
Therefore C = 160 × 3 = 480 °C·(Unit length)

We therefore have the general equation as

T =
`(480)/(√(x^2+y^2+z^2))`

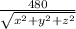
The vector from points (1, 2, 2) to point (4, 1, 3) is given by

1·i + 2·j +2·k - (4·i + 1·j +3·k) = -3·i + j -k

From which we find the unit vector given by

u =
`(1)/(√((-3)^2+1^2+(-)^2) ) (-3, 1, -1)= (1)/(√(11) ) (-3, 1, -1)`

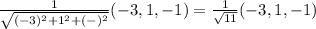
From which we have the gradient equal to

∇T(x, y, z) = -480×(x²+y²+z²)
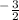`^-{(3)/(2)}` in (x, y, z)

This gives D
`_u` = ∇T·u

= -480×(x²+y²+z²)
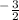`^-{(3)/(2)}` in (x, y, z)·
`(1)/(√(11) ) (-3, 1, -1)`

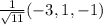
That is

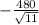`-(480)/(√(11) )`(x²+y²+z²)
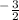`^-{(3)/(2)}` (-3·x + y - z)

From where D
`_u`Tat point (1, 2, 2) is =
`(160√(11) )/(33)`

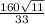
(b) The direction of greatest increase in temperature is in the direction of the gradient and the direction of the gradient is opposite to the direction of {x, y, z}, which is away from the origin.

Hence the direction of the greatest increase in temperature is towards the origin.