Question

Suppose that you were not given the sample mean and sample standard deviation and instead you were given a list of data for the speeds (in miles per hour) of the 20 vehicles. 19 19 22 24 25 27 28 37 35 30 37 36 39 40 43 30 31 36 33 35 How would you use the data to do this problem?

Answer 1

So, the sample mean is 31.3.

So, the sample standard deviation is 6.98.

Explanation:

We have a list of data for the speeds (in miles per hour) of the 20 vehicles. So, N=20.

We calculate the sample mean :

`\mu=(19 +19 +22 +24 +25 +27 +28+ 37 +35 +30+ 37+ 36+ 39+ 40+ 43+ 30+ 31+ 36+ 33+ 35)/(20)\\\\\mu=(626)/(20)\\\\\mu=31.3`

So, the sample mean is 31.3.

We use the formula for a sample standard deviation:

`\sigma=\sqrt{(1)/(N-1)\sum_(i=1)^(N)(x_i-\mu)^2}`

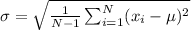
Now, we calculate the sum

`\sum_(i=1)^(20)(x_i-31.3)^2=(19-31.3)^2+(19-31.3)^2+(22-31.3)^2+(24-31.3)^2+(25-31.3)^2+(27-31.3)^2+(28-31.3)^2+(37-31.3)^2+(35-31.3)^2+(30-31.3)^2+(37-31.3)^2+(36-31.3)^2+(39-31.3)^2+(40-31.3)^2+(43-31.3)^2+(30-31.3)^2+(31-31.3)^2+(36-31.3)^2+(33-31.3)^2+(35-31.3)^2\\\\\sum_(i=1)^(20)(x_i-31.3})^2=926.2\\`

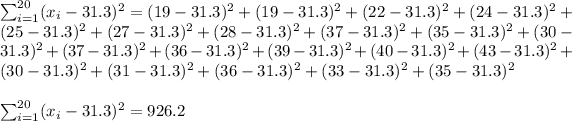
Therefore, we get

`\sigma=\sqrt{(1)/(N-1)\sum_(i=1)^(N)(x_i-\mu)^2}\\\\\sigma=\sqrt{(1)/(19)\cdot926.2}\\\\\sigma=6.98`

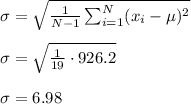
So, the sample standard deviation is 6.98.