Question

In peas, a gene controls flower color such that R = purple and r = white. In an isolated pea patch, there are 36 purple-flowering plants and 64 white-flowering plants. Assuming Hardy-Weinberg equilibrium, what is the value of q for this population?

Answer 1

Answer: q=0.8

Step-by-step explanation: The principle of Hardy-weinberg states that if no evolutionary factor interferes in a population, the frequency of the alleles would be the same for future generations. To be in equilibrium, the population has to be very big and the crossing between two different individuals has to occur randomly.

If this is the case and there are no mutations, migrations or selection, the population is in genetic equilibrium.

To calculate alleles' frequency in these conditions, the principle stabilishes that for a known pair of alleles with frequency p and q, in which p is for dominant allele and q is for recessive, the frequency of genotype in each generation is
`p^(2) + 2pq + q^(2) =1`

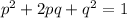
Now, to find the value of q:

Total of individual: 36+64=100

q is the frequency of recessive genotype, so:

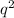`q^(2)` =
`(64)/(100)`

q =
`\sqrt{(64)/(100) }`

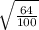
q = 0.8 or 80%

The value of q for this population in Hardy-Weinberg equilibrium is q=0.8