Question

A political polling agency wants to take a random sample of registered voters and ask whether or not they will vote for a certain candidate. One plan is to select 400 voters, another plan is to select 1,600 voters. Which one of the following is true regarding the standard deviation of the sampling distribution of the sample proportion, ^ p , of "yes" responses? The standard deviation of the sampling distribution will be 4 times smaller with sample size 400. The standard deviation of the sampling distribution will be 4 times larger with sample size 400. The standard deviation of the sampling distribution will be 2 times smaller with sample size 400. The standard deviation of the sampling distribution will be 2 times larger with sample size 400. The standard deviation of the sampling distribution will be the same for both sample sizes.

Answer 1

The standard deviation of the sampling distribution will be 2 times larger with sample size 400.

Explanation:

The standard deviation of the sampling distribution of the sample proportion is:

`SD(\hat p)=\sqrt{( p(1-p))/(n)}`

For the sample size n₁ = 400 compute the standard deviation of sample proportion as follows:

`SD_(1)(\hat p)=\sqrt{( p(1-p))/(n_(1))}=\sqrt{( p(1-p))/(400)}=(1)/(20)√( p(1-p))`

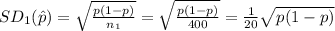
For the sample size n₂ = 1600 compute the standard deviation of sample proportion as follows:

`SD_(2)(\hat p)=\sqrt{( p(1-p))/(n_(2))}=\sqrt{( p(1-p))/(1600)}=(1)/(40)√( p(1-p))`

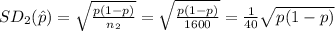
So the relation between the two standard deviations is:

`SD_(2)=(1)/(2) SD_(1)`

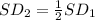
So the standard deviation for size 400 is 2 times larger than the standard deviation with size 1600.

Thus, the standard deviation of the sampling distribution will be 2 times larger with sample size 400.