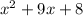The area of the rectangle in standard form is
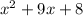
Step-by-step explanation:
Given that the length of the rectangle is
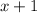
The width of the rectangle is
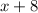
We need to determine the area of the rectangle.
The area of the rectangle can be determined using the formula,
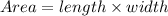
Substituting the values of length and width in the formula, we get,
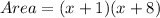
Multiplying the terms, we get,
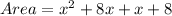
Adding the like terms, we have,
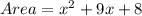
Thus, the area of the rectangle in standard form is