Answer:
12.84 miles per hour
Step-by-step explanation:
Given:
Vertical distance of starting point of van from Springfield (d) = 152 miles
Speed in east direction (s) = 25 mph
Distance traveled in east direction (e) = 91 miles
Let the direct distance from Springfield of the van be 'x' at any time 't'.
Now, from the question, it is clear that, the vertical distance of van is fixed at 152 miles and only the horizontal distance is changing with time.
Now, consider a right angled triangle SNE representing the given situation.
Point S represents Springfield, N represents the starting point of van and E represents the position of van at any time 't'.
SN = d = 152 miles (fixed)
Now, using the pythagorean theorem, we have:
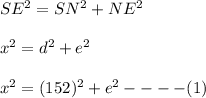
Now, differentiating both sides with respect to time 't', we get:

Now, we are given speed as 25 mph. So,
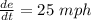
Also, when
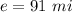 , we can find 'x' using equation (1). This gives,
, we can find 'x' using equation (1). This gives,
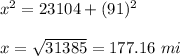
Now, plug in the values of 'e' and 'x' and solve for
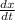 . This gives,
. This gives,
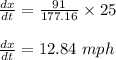
Therefore, the distance between the van and Springfield is changing at a rate of 12.84 miles per hour