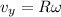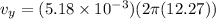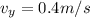Answer:
The maximum transverse speed of the bead is 0.4 m/s
Step-by-step explanation:
As we know that the Amplitude of the travelling wave is
A = 3.65 mm
Now the speed of the travelling wave is
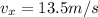
now we know that distance of first antinode from one end is 27.5 cm
so length of the loop of the standing wave is given as

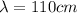
now we have

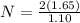
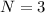
now we have

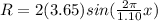
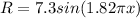
now at x = 13.8 cm

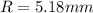
now we have
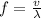
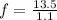
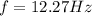
now maximum speed is given as