Question

Question 8: In a certain country, the probability that a woman reaches the age of 70 is 0.7 and the probability that a woman lives to be 80 is 0.5. (a) If a woman from that country is 70 years old, what is the conditional probability that she will survive to 80 years

Answer 1

71.43% conditional probability that she will survive to 80 years

Explanation:

We have these two following events.

Event A:

Living to be 70. So P(A) = 0.7

Event B:

Living to be 80. So P(B) = 0.5

The conditional probability formula is given by:

`P(B|A) = (P(A \cap B))/(P(A))`

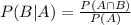
In which P(B|A) is the probability of B happening given that A has happened and
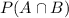`P(A \cap B)` is the probability of both events happening.

(a) If a woman from that country is 70 years old, what is the conditional probability that she will survive to 80 years

If a person lives to be 80, she must have lived to be 70. So
`P(A \cap B) = 0.5`

`P(B|A) = (P(A \cap B))/(P(A)) = (0.5)/(0.7) = 0.7143`

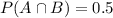
71.43% conditional probability that she will survive to 80 years