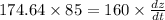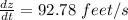Question

A police car is located 70 feet to the side of a straight road. A red car is driving along the road in the direction of the police car and is 160 feet up the road from the location of the police car. The police radar reads that the distance between the police car and the red car is decreasing at a rate of 85 feet per second. How fast is the red car actually traveling along the road

Answer 1

Actual speed of red car is 92.78 feet/s

Step-by-step explanation:

Consider A be the position of police car, B is the point of road from which the distance of police car measure and C is the point from which the red car is moving towards the point B as shown in the figure.

According to the figure,

AB = x, BC = z and AC = y.

According to the problem,

Distance between road and police car, x = 70 feet

Distance between police car and red car, y = 160 feet

Using Pythagoras theorem in the following figure,

(AC)² = (AB)² + (BC)²

y² = x² + z² ....(1)

Substitute the suitable values in the above equation.

y² = (160)² + (70)²

y = √30500

y = 174.64 feet

Differentiating equation (1) with respect to time t:

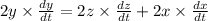`2y*(dy)/(dt)=2z*(dz)/(dt)+2x*(dx)/(dt)` ...(2)

According to the problem,

Position of police car is fixed with respect to road, so
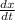`(dx)/(dt)` is zero and

Distance between police car and red car is decreasing,
`(dy)/(dt) = 85\ feet/s`

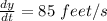
Hence equation (2) becomes:

`y*(dy)/(dt)=z*(dz)/(dt)`

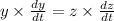
Substitute the suitable values in the above equation.

`174.64*85=160*(dz)/(dt)`

`(dz)/(dt)=92.78\ feet/s`