Question

A 20-foot tall flagpole is leaning towards a house. If the flagpole makes an 85 degree angle with the ground and the angle of elevation from the base of the house to the top of the pole is 55 degrees, find the distance from the base of the flagpole to the house

Answer 1

To find the distance from the base of the flagpole to the house, use trigonometry with the angle of elevation and the height of the flagpole.

Step-by-step explanation:

To find the distance from the base of the flagpole to the house, we can use trigonometry.

Let's call the distance from the base of the flagpole to the house x.

Using the angle of elevation of 55 degrees, we can set up the following equation:

tan(55) = x / 20

Solving for x, we find that x = 20 * tan(55).

Plugging this into a calculator, we get x ≈ 27.2 feet.

Therefore, the distance from the base of the flagpole to the house is approximately 27.2 feet.

Answer 2

Approximately, there is a distance of 25,6 foot between the base of the flagpole to the house.

Step-by-step explanation:

We are given the following in the question:

Height of pole = 20 foot

Angle between pole and ground = 85 degrees

Angle of elevation from the base of the house to the top of the pole = 55 degrees

Then, the third angle of the triangle can be found as:

Angle sum property of triangle: The sum of the three angles of a triangle is 180 degrees.

`x + 85 + 55 = 180\\x = 180 - 140\\x = 40^\circ`

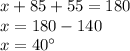
Thus, by the sin rule, we can write:

`\frac{\text{Distance from the base of the flagpole to the house}}{\sin 55} = (20)/(\sin 40)\\\\\Rightarrow \text{Distance from the base of the flagpole to the house} = 20* (\sin 55)/(\sin 40)\\\\=20* (0.82)/(0.64) = 25.625`

Approximately, there is a distance of 25,6 foot between the base of the flagpole to the house.