Question

At a large department store, the number of years of employment for a cashier is a normally distributed variable with a mean of 5.7 years and a standard deviation of 1.8 years. If an employee is picked at random, what is the probability that the employee has worked at the store for over 10 years?

Answer 1

0.0084

Step-by-step explanation:

For this probability problem, we will have to make use of the normal probability distribution table.

to use the table, we will have to compute a certain value

z = (x- mean) /Standard deviation

z =
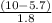`((10 - 5.7))/(1.8)` = 2.39

Probability he has worked in the store for over 10 years can be obtained by taking the z value of 2.39 to the normal probability distribution table to read off the values.

To do this, on the "z" column, we scan down the value 2.3. we then trace that row until we reach the value under the ".09" column.

This gives us 0.99916

Thus we have P (Z < 2.39) = 0.9916

We subtract the value obtained from the table from 1 to get the probability required.

1 - 0.9916 = 0.0084

The Probability that the employee has worked at the store for over 10 years = 0.0084