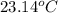Question

You heat a 5.2 gram lead ball (specific heat capacity = 0.128 Joules/g-deg) to 183. ∘ C. You then drop the ball into 34.5 milliliters of water (density 1 g/ml; specific heat capacity = 4.184 J/g-deg ) at 22.4 ∘ C. What is the final temperature of the water when the lead and water reach thermal equilibrium?

Answer 1

The final temperature when the lead and water reach thermal equilibrium is
`23.14^(o) C`

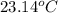
Step-by-step explanation:

Using the law of conservation of energy the heat lost by the lead ball is gained by the water.

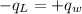`-q_(L) =+q_(w)` .............................1

where

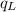`q_(L)` is the heat energy of the lead ball;

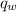`q_(w)` is the heat energy of water;

but q = msΔ

T...............................2

substituting expression in equation 2 into the equation 1;

Δ

T =Δ

T .............................3

where
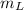`m_(L)` is the mass of the lead ball = 5.2 g

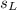`s_(L)` is the specific heat capacity of the lead ball = 0.128 Joules/g-deg

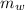`m_(w)` is the mass of water = volume x density = 34.5 ml x 1 g/ml = 34.5 g

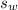`s_(w)` is the specific heat capacity of water = 4.184 J/g-deg

Δ

T is the temperature changes encountered by the lead ball and water respectively

inputting the values of the parameters into equation 3

5.2 g x 0.128 Joules/g-deg x (183-22.4) = 34.5 g x 4.184 J/g-deg x (
`T_(2)` -22.4)

`T_(2)` -22.4 =
`(106.9)/(144.3)`

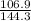
`T_(2)` -22.4 = 0.7408

`T_(2)` =
`23.14^(o) C`

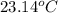
Therefore the final temperature when the lead and water reach thermal equilibrium is
`23.14^(o) C`