Question

A particle in the first excited state of a one-dimensional infinite potential energy well (with U = 0 inside the well) has an energy of 6.0 eV. What is the energy of this particle in the ground state?

Answer 1

The energy of this particle in the ground state is E₁=1.5 eV.

Step-by-step explanation:

The energy
`E_(n)` of a particle of mass m in the nth energy state of an infinite square well potential with width L is:

`E_(n)=(n^(2)h^(2))/(8mL^(2))`

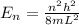
In the ground state (n=1). In the first excited state (n=2) we are told the energy is E₂= 6.0 eV. If we replace in the above equation we get that:

`E_(1)=(h^(2))/(8mL^(2))`

`E_(2)=(h^(2))/(2mL^(2))`

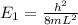
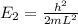
So we can rewrite the energy in the ground state as:

`E_(1)=(1)/(4)((h^(2))/(2mL^(2)))`

`E_(1)=(1)/(4) E_(2)`

`E_(1)=(1)/(4) ( 6.0\ eV)`

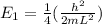
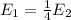
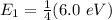
Finally

`E_(1)=1.5\ eV`