The formula
 represents the geometric sequence.
represents the geometric sequence.
Explanation:
Step 1:
The value of
 is dependent on the value of n.
is dependent on the value of n.
So n is independent while
 is dependent on n i.e. the value of
is dependent on n i.e. the value of
 depends on the value of n.
depends on the value of n.
Step 2:
We substitute the values of n in the functions to check which function satisfies the values of
 .
.
If
 This does not equal the value of
This does not equal the value of
 .
.
If
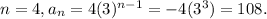 This does not equal the value of
This does not equal the value of
 .
.
If
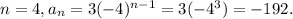 This does not equal the value of
This does not equal the value of
 .
.
If
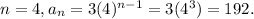 This equals the value of
This equals the value of
 .
.
So the fourth formula represents the geometric sequence.