Question

Please solve and explain. Photo attached

Answer 1

`$((x+1)(x-3))/(x^(2))`

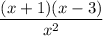
Solution:

Given expression:

`$((36)/(x^(2))+(36)/(x))/((36)/(x-3))`

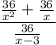
To solve this expression:

`$((36)/(x^(2))+(36)/(x))/((36)/(x-3))`

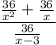
Apply the fraction rule:
`$(a)/((b)/(c))=(a \cdot c)/(b)`

`$=(\left((36)/(x^(2))+(36)/(x)\right)(x-3))/(36)`

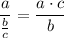
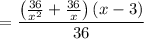
Let us solve
`(36)/(x^(2))+(36)/(x)`.

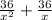Least common multiple of
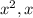`x^(2), x` is
`x^(2)`.

Make the denominator same based on the LCM.

So that multiply and divide the 2nd term by x, we get

`$(36)/(x^(2))+(36)/(x)=(36)/(x^(2))+(36 x)/(x^(2))`

`$=(36+36 x)/(x^(2))`

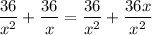
Now, multiply by (x - 3).

`$(36+36 x)/(x^(2))(x-3)= ((36 x+36)(x-3))/(x^(2))`

`$(\left((36)/(x^(2))+(36)/(x)\right)(x-3))/(36)=(((36 x+36)(x-3))/(x^(2)))/(36)`

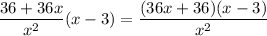
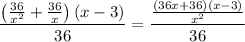
Apply the fraction rule:
`((b)/(c))/(a)=(b)/(c \cdot a)`

`$=((36x+36)(x-3))/(x^(2) \cdot 36)`

`$=(36(x+1)(x-3))/(x^(2) \cdot 36)`

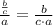
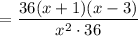
Cancel the common factor 36.

`$=((x+1)(x-3))/(x^(2))`

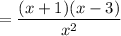
Hence the solution is
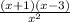`((x+1)(x-3))/(x^(2))`.