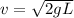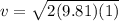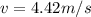Question

A meter stick with a mass of 0.167 kg is pivoted about one end so it can rotate without friction about a horizontal axis. The meter stick is held in a horizontal position and released. As it swings through the vertical, calculate:

a. The change in gravitational potential energy that has occurred.
b. The angular speed of the stick.
c. The linear speed of the end of the stick opposite the axis.
d. Compare the answer in part (c) to the speed of a particle that has fallen 1.00 m, starting from rest.

Answer 1

Part a)

change in potential energy is given as

`\Delta U = 0.82 J`

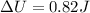
Part B)

angular speed of the rod is given as

`\omega = 5.42 rad/s`

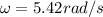
Part c)

Linear speed of the end of the rod is given as

`v = 5.42 m/s`

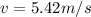
Part d)

when a particle falls from rest to distance d = 1 m

`v = 4.42 m/s`

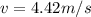
Step-by-step explanation:

Part A)

As we know that the gravitational potential energy change is given as

`\Delta U = mgH`

`\Delta U = 0.167(9.81)(0.5)`

`\Delta U = 0.82 J`

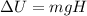
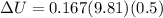
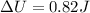
Part B)

As we know that change in gravitational energy is equal to gain in kinetic energy

so we have

`\Delta U = (1)/(2)I\omega^2`

`0.82 = (1)/(2)((mL^2)/(3))\omega^2`

`\omega^2 = (6 * 0.82)/(0.167 (1)^2)`

`\omega = 5.42 rad/s`

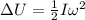
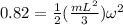
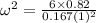
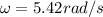
Part c)

Linear speed of the end of the rod is given as

`v = L\omega`

`v = 5.42 m/s`

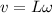
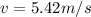
Part d)

when a particle falls from rest to distance d = 1 m

so we will have

`v = √(2gL)`

`v = √(2(9.81)(1))`

`v = 4.42 m/s`