Question

The 2003 Zagat Restaurant Survey provides food, decor, and service ratings for some of the top restaurants across the United States. For 15 top-ranking restaurants located in Boston, the average price of a dinner, including one drink and tip, was $48.60. You are leaving on a business trip to Boston and will eat dinner at three of these restaurants. Your company will reimburse you for a maximum of $50 per dinner. Business associates familiar with the restaurants have told you that the meal cost at 5 of the restaurants will exceed $50. Suppose that you randomly select three of these restaurants for dinner. What is the probability that none of the meals will exceed the cost covered by your company (to 4 decimals)

Answer 1

The probability that none of the meals will exceed the cost covered by your company is 0.2637.

Explanation:

A hyper-geometric distribution is used to define the probability distribution of k success in n samples drawn from a population of size N which include K success. Every draw is either a success of failure.

The random variable X = number of meals that will exceed the cost covered by the company.

The random variable X follows a hyper-geometric distribution.

The information provided is:

N = 15

K = 3

n = 5

k = 0

The probability mass function of a hyper-geometric distribution is:

`P(X=k)=\frac{{K\choose k}{N-K\choose n-k}}{{N\choose n}}`

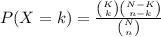
Compute the probability that none of the meals will exceed the cost covered by your company as follows:

`P(X=0)=\frac{{3\choose 0}{15-3\choose 5-0}}{{15\choose 5}}=(1* 792)/(3003)=0.2637`

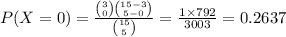
Thus, the probability that none of the meals will exceed the cost covered by your company is 0.2637.