Answer:
The probability that a randomly selected member of the labor force is African American given that he or she is unemployed is 0.2308.
Step-by-step explanation:
The events are denoted as:
A = a member of a labor force is African American
B = a member of a labor force is unemployed
The information provided is:
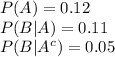
The Bayes' theorem states that the conditional probability of an event E given that another event X has already occurred is:
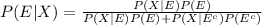
Use the Bayes' theorem to compute the value of P (A|B) as follows:
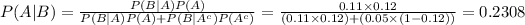
Thus, the probability that a randomly selected member of the labor force is African American given that he or she is unemployed is 0.2308.