Answer:
(a) The mean is 52 and the median is 55.
(b) The first quartile is 44 and the third quartile is 60.
(c) The value of range is 33 and the inter-quartile range is 16.
(d) The variance is 100.143 and the standard deviation is 10.01.
(e) There are no outliers in the data set.
(f) Yes
Explanation:
The data provided is:
S = {55, 56, 44, 43, 44, 56, 60, 62, 57, 45, 36, 38, 50, 69, 65}
(a)
Compute the mean of the data as follows:
![\bar x=(1)/(n)\sum x\\=(1)/(15)[55+ 56+ 44+ 43+ 44+ 56+ 60+ 62+ 57+ 45 +36 +38 +50 +69+ 65]\\=(780)/(15)\\=52](https://img.qammunity.org/2021/formulas/mathematics/college/zr1jbygwcio0874rawr2qnjw21cyad7gr8.png)
Thus, the mean is 52.
The median for odd set of values is the computed using the formula:
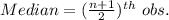
Arrange the data set in ascending order as follows:
36, 38, 43, 44, 44, 45, 50, 55, 56, 56, 57, 60, 62, 65, 69
There are 15 values in the set.
Compute the median value as follows:
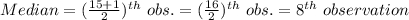
The 8th observation is, 55.
Thus, the median is 55.
(b)
The first quartile is the middle value of the upper-half of the data set.
The upper-half of the data set is:
36, 38, 43, 44, 44, 45, 50
The middle value of the data set is 44.
Thus, the first quartile is 44.
The third quartile is the middle value of the lower-half of the data set.
The upper-half of the data set is:
56, 56, 57, 60, 62, 65, 69
The middle value of the data set is 60.
Thus, the third quartile is 60.
(c)
The range of a data set is the difference between the maximum and minimum value.
Maximum = 69
Minimum = 36
Compute the value of Range as follows:
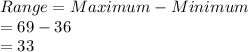
Thus, the value of range is 33.
The inter-quartile range is the difference between the first and third quartile value.
Compute the value of IQR as follows:
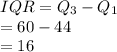
Thus, the inter-quartile range is 16.
(d)
Compute the variance of the data set as follows:
![s^(2)=(1)/(n-1)\sum (x_(i)-\bar x)^(2)\\=(1)/(15-1)[(55-52)^(2)+(56-52)^(2)+...+(65-52)^(2)]\\=100.143](https://img.qammunity.org/2021/formulas/mathematics/college/i6oo7ahs7tdecfde9mxlmj4swb7v5hejih.png)
Thus, the variance is 100.143.
Compute the value of standard deviation as follows:
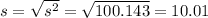
Thus, the standard deviation is 10.01.
(e)
An outlier is a data value that is different from the remaining values.
An outlier is a value that lies below 1.5 IQR of the first quartile or above 1.5 IQR of the third quartile.
Compute the value of Q₁ - 1.5 IQR as follows:

Compute the value of Q₃ + 1.5 IQR as follows:
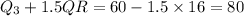
The minimum value is 36 and the maximum is 69.
None of the values is less than 20 or more than 80.
Thus, there are no outliers in the data set.
(f)
Yes, the data provided indicates that the Walmart is meeting its goal for reducing the number of hourly employees