Question

The flywheel of a steam engine begins to rotate from rest with a constant angular acceleration of 1.35 rad/s2. It accelerates for 28.3 s, then maintains a constant angular velocity. Calculate the total angle through which the wheel has turned 58.9 s after it begins rotating.

Answer 1

Total angle through which the wheel has turned 58.9s after it begins rotating is 1709.52 rad

Step-by-step explanation:

The image attached would offer a better explanation

Answer 2

The answer to the question is;

The total angle through which the wheel has turned 58.9 s after it begins rotating is approximately 1709.67 rad.

Step-by-step explanation:

To solve the question we note the equation for the motion of the flywheel as

ω₂ = ω₁ + α·t

Where:

ω₁ = Initial angular velocity = 0 rad/s as the body is initially at rest

ω₂ = Final angular velocity

α = angular acceleration = 1.35 rad/s²

t = Time = 28.3 s

Plugging in the values, we find ω₂

ω₂ = 0 + 1.35 rad/s²× 28.3 s = 38.205 rad/s

Since the acceleration is constant, only the mean velocity is required to determine the angle traveled during the first 28.3 seconds thus

Average velocity

ω
`_(average)`=
`(Final .Velocity +Initial . Velocity)/(2) = (\omega_2+\omega_1)/(2) = (38.205 rad/s+0 rad/s)/(2)`

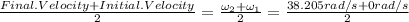
= 19.1025 rad/s

The total angle traveled in 28.3 s is ω
`_(average)` × time

= 19.1025 rad/s × 28.3 s = 540.60075 rad

After this the remaining time left is

58.9 s - 28.3 s = 30.6 s

Since the flywheel is moving at a constant velocity of 38.205 rad/s during the last 30.6 s we have

Angle traveled in 30.6 s at an angular velocity of 38.205 rad/s is given by

Angle traveled = Time × Angular velocity = 30.6 s × 38.205 rad/s

= 1169.073 rad

Therefore, the total angle traveled by the flywheel in 58.9 s is given by

540.60075 rad + 1169.073 rad = 1709.67375 rad ≈1709.67 rad.

the total angle traveled by the flywheel in 58.9 s ≈ 1709.67 rad.