Question

The temperature at a point (x,y,z) is given by T(x,y,z)=200e^-x^2-3y^-9z^2, where T measured in degrees Celsius and x,y,z in meters. Find the rate of change of temperature at the point P(2, -1, 2) in the direction toward the point (3, -3, 3)

Answer 1

Therefore the rate change of temperature at the point P(2,-1,2) in the direction toward the point (3,-3,3) is
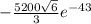`-(5200\sqrt6)/(3)e^(-43)` °C/m.

Explanation:

Given that, the temperature at a point (x,y,z) is

`T(x,y,z)=200e^(-x^2-3y^2-9z^2)`.

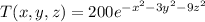Rate change of temperature at the point P(2,-1,2) in the direction toward the point Q (3,-3,3) is
`D_uT(2,-1,2)`

`T_x= 200(-2x)e^(-x^2-3y^2-9z^2)`
`=-400x200.2xe^(-x^2-3y^2-9z^2)`

`T_y = 200.(-6y)e^(-x^2-3y^2-9z^2)`
`=-1200ye^(-x^2-3y^2-9z^2)`

`T_z=200(-18z)e^(-x^2-3y^2-9z^2)`
`=-3600ze^(-x^2-3y^2-9z^2)`

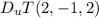
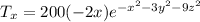
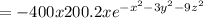
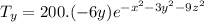
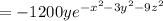
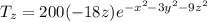
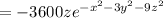
The gradient of the temperature

`\bigtriangledown T(x,y,z)= (-400x200.2xe^(-x^2-3y^2-9z^2),-1200ye^(-x^2-3y^2-9z^2),-3600ze^(-x^2-3y^2-9z^2))`
`=-400e^(-x^2-3y^2-9z^2)(x,3y,9z)`

`\bigtriangledown T(2,-1,2) = -400e^(-2^2-3(-1)^2-9.2^2)(2,3.(-1),9.2)`

`=-400 e^(-43)(2,-3,18)`

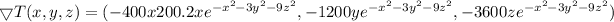
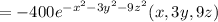
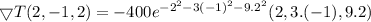
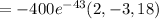
V=
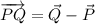`\overrightarrow {PQ}= \vec{Q}-\vec{P}`=(3,-3,3)-(2,-1,2)=(1,-2,1)

The unit vector of V is
`((1,-2,1))/(√(1^2+(-2)^2+1^2))`

`=(1)/(\sqrt6)(1,-2,1)`

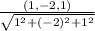
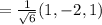
Therefore,

`D_uT(2,-1,2) = \bigtriangledown T(2,-1,2).(1)/(\sqrt6)(1,-2,1)`

`=-400 e^(-43)(2,-3,18).(1)/(\sqrt6)(1,-2,1)`

`=-(400)/(\sqrt6)e^(-43)(2.1+(-3).(-2)+18.1)`

`=-(10400)/(\sqrt6)e^(-43)`

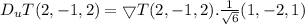
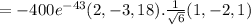
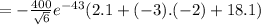
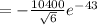
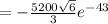`=-(5200\sqrt6)/(3)e^(-43)` °C/m

Therefore the rate change of temperature at the point P(2,-1,2) in the direction toward the point (3,-3,3) is
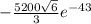`-(5200\sqrt6)/(3)e^(-43)` °C/m.