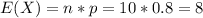Answer:
a)
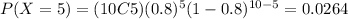
b)
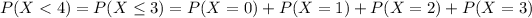
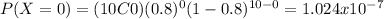
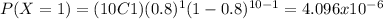
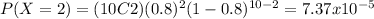
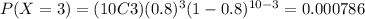
And adding we got:
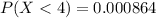
c)
![P(X \geq 6) = 1-P(X<6) = 1-P(X\leq 5) =1-[P(X=0) +....+P(X=5)]](https://img.qammunity.org/2021/formulas/mathematics/college/wndpxyt92skxef7txfe8mp8v2e8iff0xxe.png)
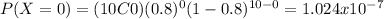
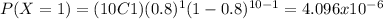
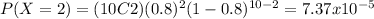
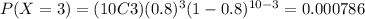
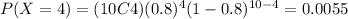
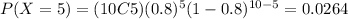
And replacing we got:
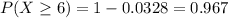
d)
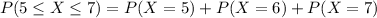
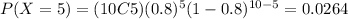
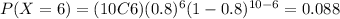
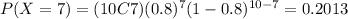
And replacing we got:
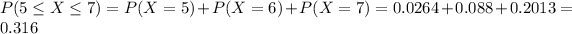
e)
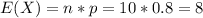
Explanation:
Previous concepts
The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".
Solution to the problem
Let X the random variable of interest, on this case we now that:
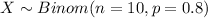
The probability mass function for the Binomial distribution is given as:
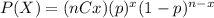
Where (nCx) means combinatory and it's given by this formula:
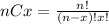
Part a
We want to find this probability:
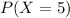
And using the pmf we got:
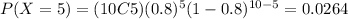
Part b
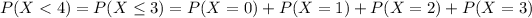
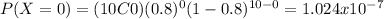
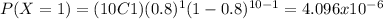
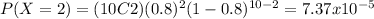
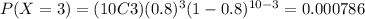
And adding we got:
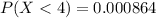
Part c
For this case we can use the complement rule like this:
![P(X \geq 6) = 1-P(X<6) = 1-P(X\leq 5) =1-[P(X=0) +....+P(X=5)]](https://img.qammunity.org/2021/formulas/mathematics/college/wndpxyt92skxef7txfe8mp8v2e8iff0xxe.png)
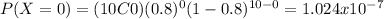
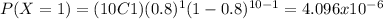
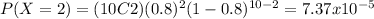
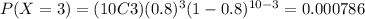
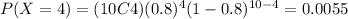
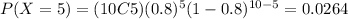
And replacing we got:
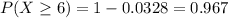
Part d
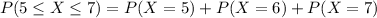
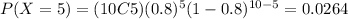
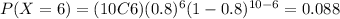
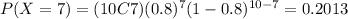
And replacing we got:
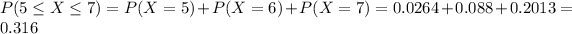
Part e
The expected number is given by: