Question

An electron is traveling east with an instantaneous velocity of 3.3 × 105 m/s when it enters a uniform magnetic field of 0.25 T that points X degrees north of east. (Take east as to the right of the paper and north as toward the top of the paper, i.e., both in the plane of the paper.) If the magnitude of the force on the electron is 5.5 × 10–15 N, then calculate the angle X and whether the electron moves up out of or down into the plane of the page, or otherwise.

Answer 1

To solve this problem we will apply the concepts related to the electromagnetic force, in which this is specified as the product between the speed of the electron, the magnetic field, the charge of the electron and the sine of the angle that occurs between the electric field and the stream. Mathematically the simplified expression can be written as

`F = BqVsin\theta`

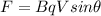
Our values are given as,

`\text{Velocity of Electron} = V = 3.3*10^5m \cdot s^(-1)`

`\text{Magnetic Field} = B = 0.25T`

`\text{Force on electron} = F = 5.5*10^(-15)N`

`\text{Charge of electron} = q = 1.6*10^(-19) C`

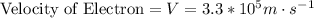
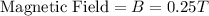
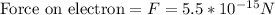
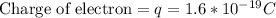
Rearranging the expression to find the angle we have,

`\theta = sin^(-1) ((F)/(BqV))`

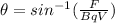
Replacing,

`\theta = sin^(-1) ((5.5*10^(-15))/((0.25)(1.6*10^(-19))(3.3*10^5)))`

`\theta = 24.58\° \approx 25\°`

Therefore the angle is 25° and goes down into the page (Right hand rule)