Question

A runner taking part in the 200 m dash must run around the end of a track that has a circular arc with a radius of curvature of 40 m. If he completes the 200 m dash in 24.0 s and runs at constant speed throughout the race, what is the magnitude of his centripetal acceleration (in m/s2) as he runs the curved portion of the track?

Answer 1

The centripetal acceleration of the runner is
`1.73\ m/s^2`.

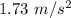Step-by-step explanation:

Given that,

A runner completes the 200 m dash in 24.0 s and runs at constant speed throughout the race. We need to find the centripetal acceleration as he runs the curved portion of the track. We know that the centripetal acceleration is given by :

`a=(v^2)/(r)`

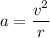
v is the velocity of runner

`v=(200\ m)/(24\ s)\\\\v=8.34\ m/s`

Centripetal acceleration,

`a=((8.34)^2)/(40)\\\\a=1.73\ m/s^2`

So, the centripetal acceleration of the runner is
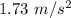`1.73\ m/s^2`. Hence, this is the required solution.