Answer:
The man will take 64 seconds to reach to the south shore of the frozen pond.
Explanation:
Given:
Weight of the man = 748 N Mass of the man,
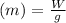 =
=
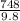 =
=
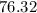 kg
kg
Radius of the pond
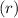 = 4 m
= 4 m
Mass of the textbook = 1.2 kg
Velocity at which the textbook is thrown = 4 ms^1
We have to find the velocity of the man after the throw.
Let the velocity is
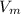 .
.
Now using law of conservation of momentum we can find the
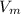 value.
value.
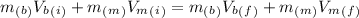
Considering
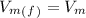
And initial velocity of both the man and book i.e
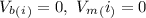
So,
⇒
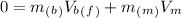
⇒ Plugging the values.
⇒

⇒
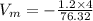
⇒
 ms^-1
ms^-1
Here the negative velocity is meant for opposite direction of the throw.
Numerically we will write,
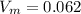
With this velocity the man will move towards south.
We have to calculate the time taken by the man to move to its south shore.
And we know
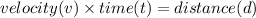
Let the time taken be
 and
and
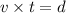 and
and
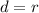 then,
then,
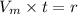
Then
⇒
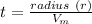
⇒ Plugging the values.
⇒

⇒
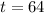 sec
sec
The man will take 64 seconds to reach to the south shore of the frozen pond (circular).