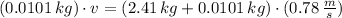Question

A(n) 10.1 g bullet is fired into a(n) 2.41 kg ballistic pendulum and becomes embedded in it. The acceleration of gravity is 9.8 m/s 2 . If the pendulum rises a vertical distance of 3.12 cm, calculate the initial speed of the bullet

Answer 1

`v = 186.90\,(m)/(s)`

Step-by-step explanation:

The motion of ballistic pendulum is modelled by the appropriate use of the Principle of Energy Conservation:

`(1)/(2)\cdot (m_(p)+m_(b))\cdot v^(2) = (m_(p)+m_(b))\cdot g \cdot h`

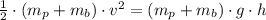
The final velocity of the system formed by the ballistic pendulum and the bullet is:

`v = √(2\cdot g\cdot h)`

`v = \sqrt{2\cdot (9.807\,(m)/(s^(2)) )\cdot (0.031\,m)}`

`v\approx 0.78\,(m)/(s)`

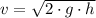
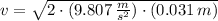
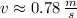
Initial velocity of the bullet can be calculated from the expression derived of the Principle of Momentum:

`(0.0101\,kg)\cdot v = (2.41\,kg + 0.0101\,kg)\cdot (0.78\,(m)/(s) )`

`v = 186.90\,(m)/(s)`