Question

5) Fill in the gaps in this sequence: -8, -19.-30,_ , _ .

a. What type of sequence is this, Geometric or Arithmetic? Explain.
yol surtis
b. Write an explicit formula for this sequence.
c. Write a recursive formula for this sequence.
' et bil
d. Find the 30th term.

Answer 1

The missing two terms are -41 and -52

a. The sequence is arithmetic

b. The explicit formula for the sequence is
`a_(n)=3-11n`

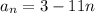
c. The recursive formula for this sequence is
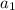`a_(1)` = -8;
`a_(n)` =
`a_(n-1)` + -11

d. The 30th term is -327

Explanation:

The terms of the sequence are -8 , -19 , -30

∵ -19 - (-8) = -19 + 8 = -11

∵ -30 - (-19) = -30 + 19 = -11

- That means there is a constant difference between each two

consecutive terms

∴ -30 + -11 = -41

∴ -41 + -11 = -52

∴ The missing two terms are -41 and -52

a.

∵ There is a constant difference between each two

consecutive terms

∴ The sequence is arithmetic

b.

The explicit formula of the nth term of an arithmetic sequence is
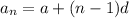`a_(n)=a+(n-1)d`, where a is the first term and d is the constant difference between each two consecutive term

∵ The first term is -8

∴ a = -8

∵ The constant difference is -11

∴ d = -11

- Substitute them in the formula above

∴
`a_(n)=-8+(n-1)(-11)`

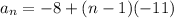
- Simplify it by multiplying (n - 1) times -11

∴
`a_(n)=-8-11n+11`

∴
`a_(n)=3-11n`

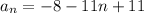
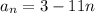
∴ The explicit formula for the sequence is
`a_(n)=3-11n`

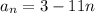
c.

The recursive formula of the arithmetic sequence is:

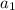`a_(1)` = first term;
`a_(n)` =
`a_(n-1)` + d, where d is the common difference between each two consecutive terms

∵ The first term is -8

∴
`a_(1)=-8`

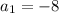
∵ The constant difference is -11

∴ d = -11

∴
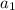`a_(1)` = -8;
`a_(n)` =
`a_(n-1)` + -11

∴ The recursive formula for this sequence is
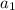`a_(1)` = -8;
`a_(n)` =
`a_(n-1)` + -11

d.

∵ The term is 30th

∴ n = 30

- Substitute it in the explicit formula of the sequence

∴
`n_(30)=3 - 11(30)`

∴
`n_(30)=3 - 330`

∴
`n_(30)=-327`

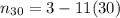
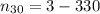
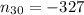
∴ The 30th term is -327