Answer:
Heat transfer during the process = 0
Work done during the process = - 371.87 KJ
Step-by-step explanation:
Initial pressure
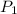 = 0.02 bar
= 0.02 bar
Initial temperature
 = 200 K
= 200 K
Final pressure
 = 0.14 bar
= 0.14 bar
Gas constant for helium R = 2.077
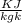
This is an isentropic polytropic process so temperature - pressure relationship is given by the following formula,
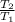 =
=
![[(P_(2) )/(P_(1) ) ]^{(\gamma - 1)/(\gamma) }](https://img.qammunity.org/2021/formulas/physics/college/5ibt8tzxlqiut8yntihmvrgnembam2oirg.png)
Put all the values in above formula we get,
⇒
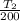 =
=
![[(0.14 )/(0.02 ) ]^{(1.4 - 1)/(1.4) }](https://img.qammunity.org/2021/formulas/physics/college/mrjkza8itsi59lo5et9dd8wgqjpemgogng.png)
⇒
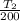 = 1.74
= 1.74
⇒
 = 348.72 K
= 348.72 K
This is the final temperature of helium.
For isentropic polytropic process heat transfer to the system is zero.
⇒ ΔQ = 0
Work done W = m × (
 -
-
 ) ×
) ×
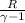
⇒ W = 1 × ( 200 - 348.72 ) ×

⇒ W = 371.87 KJ
This is the work done in this process. here negative sign shows that work is done on the gas in the compression of gas.