Question

In a fast-pitch softball game the pitcher is impressive to watch, as she delivers a pitch by rapidly whirling her arm around so that the ball in her hand moves in a circle. In one instance, the radius of the circle is 0.610 m. At one point on this circle, the ball has an angular acceleration of 67.6 rad/s2 and an angular speed of 17.0 rad/s. (a) Find the magnitude of the total acceleration (centripetal plus tangential) of the ball. (b) Determine the angle of the total acceleration relative to the radial direction.

Answer 1

(a) 181.05 m/s²

(b) 13.2°

Step-by-step explanation:

Given:

Radius of the circle (R) = 0.610 m

Angular acceleration (α) = 67.6 rad/s²

Angular speed (ω) = 17.0 rad/s

(a)

Radial acceleration of the ball is given as:

`a_r=\omega^2R`

Plug in the given values and solve for
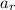`a_r`. This gives,

`a_r=(17.0\ rad/s)^2* (0.610\ m)\\\\a_r=289* 0.610\ m/s^2\\\\a_r=176.29\ m/s^2`

Now, tangential acceleration is given by the formula:

`a_t=R\alpha`

Plug in the given values and solve for
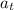`a_t`. This gives,

`a_t=(0.610\ m)(67.6\ rad/s^2)\\\\a_t=41.236\ m/s^2`

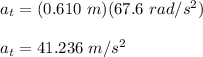
Now, the magnitude of total acceleration is given as the square root of the sum of the squares of tangential and centripetal accelerations. Therefore,

`a_(Total)=√((a_r)^2+(a_t)^2)`

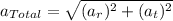
Plug in the given values and solve for total acceleration,
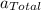`a_(Total)`. This gives,

`a_(Total)=√((176.29)^2+(41.236)^2)\\\\a_(Total)=181.05\ m/s^2`

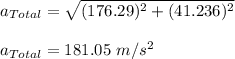
Therefore, the magnitude of total acceleration is 181.05 m/s².

(b)

Angle of total acceleration relative to radial direction is given by the formula:

`\theta=\tan^(-1)((a_t)/(a_r))\\\\\theta=\tan^(-1)((41.236)/(176.29))\\\\\theta=13.2\°`

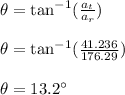
Therefore, the total acceleration makes an angle of 13.2° relative to radial direction.