Question

Light of a single color hits the wall after traveling 1.40 m from a small sliver of your window of width 0.600 mm. A diffraction pattern appears on your wall with a central maximum width of 1.15 mm. What is the wavelength of the light

Answer 1

Condition for diffraction maximum is

`dsin\theta = m\lambda`

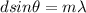
Here,

d = Distance between slits

m =Order of interference, or any integer which represent the number of repetition of the spectrum

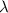`\lambda` = Wavelength

For small angles we have that

`sin\theta = tan\theta = (y)/(L)`

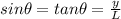
L = Distance of the Screen

y = Position on the screen

At the same time we have that the distance of the edge of central maximum is

`w = 2y`

`y = (w)/(2L)`

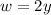
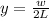
Replacing all in the first equation we have

`d((w)/(2L)) = m\lambda`

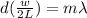
Remember that for the maximum value to be given, then the order of interference must be 1, replacing with the other values we will have to,

`(0.600*10^(-3)) ((1.15*10^(-3))/(2(1.4))) = (1) \lambda`

`\lambda =2.464*10^(-7)m`

`\lambda = 246.4nm`

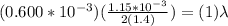
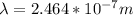
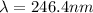
Therefore the wavelength of the light is 246.4nm