Answer:
7.2224
Explanation:
The value of the summation is given by the formula ...
Sn = (a1)(1 -r^n)/(1 -r) . . . . . where a1 is the first of n terms, and r is the common ratio.
Your sum has first term and ratio ...
a1 = 2(0.6) . . . . . summation term for n=1
r = 0.6
So the sum is ...
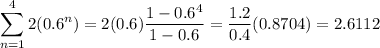
Then the value of the entire given expression is ...

_____
A calculator can help you find the value.