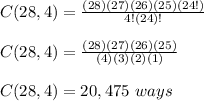Answer:
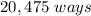
Explanation:
we know that
Combinations are a way to calculate the total outcomes of an event where order of the outcomes does not matter.
To calculate combinations, we will use the formula
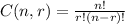
where
n represents the total number of items
r represents the number of items being chosen at a time.
In this problem
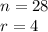
substitute
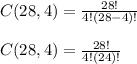
simplify