Question

What is the first quartile Q1 of the standard normal distribution? (use 3 decimal places in your answer) Question 2. What is the third quartile Q3 of the standard normal distribution? (use 3 decimal places in your answer) Question 3. What percent of the observations in the standard normal distribution are suspected outliers according to the Q1 - 1.5xIQR and Q3 + 1.5xIQR cutoff criteria that we used when constructing boxplots? (Note that this percent is the same for any normal distribution.)

Answer 1

(1) The first quartile of standard normal distribution is -0.67.

(2) The third quartile of standard normal distribution is 0.67.

(3) The percentage of the observations in the standard normal distribution that are suspected outliers is, 0.74%.

Step-by-step explanation:

A standard normal distribution has mean 0 and variance 1.

(1)

The first quartile of any data is the value below which 25% of the data lie.

That is, P (Z < z) = 0.25.

The value of z is -0.67.

Thus, the first quartile of standard normal distribution is -0.67.

(2)

The third quartile of any data is the value below which 75% of the data lie.

That is, P (Z < z) = 0.75.

The value of z is 0.67.

Thus, the third quartile of standard normal distribution is 0.67.

(3)

In case of a standard normal distribution values lying outside the range

(Q₁ - 1.5 IQR, Q₃ + 1.5 IQR)

are considered as outlier.

Compute the range as follows:

`(Q_(1) - 1.5 IQR, Q_(3) + 1.5 IQR)=[-0.67-(1.5* 1.34),\ -0.67+(1.5* 1.34)]\\=[-2.68, 2.68]`

Compute the probability of (Z < -2.68) and P (Z > 2.68) as follows:

`P(Z<-2.68)=1-P(Z<2.68)=1-0.9963=0.0037`

`P(Z>2.68)=1-P(Z<2.68)=1-0.9963=0.0037`

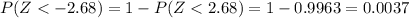
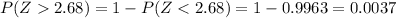
The probability of a value being an outlier is,

P (Outlier) = P (Z < -2.68) + P (Z > 2.68)

= 0.0037 + 0.0037

= 0.0074

The percentage of the observations in the standard normal distribution that are suspected outliers is, 0.0074 × 100 = 0.74%.