Question

This problem Refers to a power plant operation on an ideal Rankine steam cycle. The plant operates between the pressure limits of 1 MPa and 5.628 kPa. The temperature of the steam entering the turbines is 500oC. The total gross power generated is 300 MW. What is the quality of the steam after it has expanded in the turbines?

Answer 1

Answer is 92%.

Step-by-step explanation:

As per the question,

Pressure limits of 1 MPa and 5.628 kPa.

Temperature of the steam is 500⁰C.

(1).

s₁= s₂ (entropy)

s₂ = sf₂ + x₂ × sfg₂

7.7642 = 0.505 + x₂ × 7.845

=0.92 that is 92%.

Answer 2

Question:

Problems 1-3 refer to a power plant operating on an ideal Rankine steam cycle. The plant operates between the pressure limit of 1 MPa and 5.628 kPa. The temperature of the steam entering the turbines is 500 ⁰C the total gross power generated is 300 MW.

1 What is the quality of the steam after it has expanded in the turbines?

A. 78% B. 92% C. 97% D. 100%

2. What is the enthalpy of the steam as it enters the condenser

A. 2380 kJ/kg B. 2420 kJ/kg C. 2560 kJ/kg D. 2600 kJ/kg

3. What is the total steam flow-rate through all the turbines?

A. 10 kg/s B. 1 I 0 kg/s C. 200 kg/s D. 270 kg/s

Answer:

1. B

2. A

3. D

Step-by-step explanation:

Given Parameters

Pressures

P₁ = 1 MPa, P₂ = 5.628kPa

Temperature

T₁ = 500 ⁰C

From Steam Tables

h₁ = 3479.1 kJ/Kg, S₁ = 7.7642 kJ/Kg

When P₂= 5.628kPa,

hf = 147 kJ/Kg hfg₂ = 2413 kJ/Kg

sf = 0.505 kJ/Kg sfg₂ = 7.845 kJ/KgK

(1).

s₁= s₂ (entropy)

s₂ = sf₂ + x₂ * sfg₂

7.7642 = 0.505 + x₂ * 7.845

solving for x₂, we have x₂ = 0.92

this implies, x₂ = 92%

hence, option B is the right answer

(2).

h₂ = hf₂ + x₂ * hfg₂

= 147 + 0.92 * 2413

= 2366.96 kJ/Kg

hence, Option A is correct

(3).

let the steam flow-rate be m

from the equation

`m = (p)/(h1 - h2)`

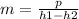
where p is the power in Watt

m = 300000 / ( 3479.1 - 2366.96)

= 269.75Kg/sec

hence option D is the right answer