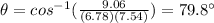a) 41.7 J
b) 4.6 W
c)
Step-by-step explanation:
a)
The work done by a force on an object is given by
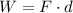
where
F is the force
d is the displacement of the object
 is the scalar product
is the scalar product
In this problem, the force is:
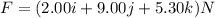
The initial position is
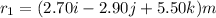
While the final position is
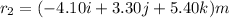
So, the displacement is the difference between r1 and r2:
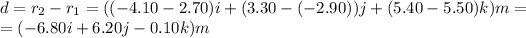
And so, the work done is:

b)
The average power is calculated as the work done divided by the time taken:
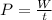
where
W is the work done
t is the time taken to do that work
In this problem:
W = 41.7 J is the work done by the force
t = 9.10 s is the time taken for this work to be done
Therefore, the power used is:
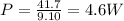
c)
Given two vectors
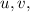 the angle between the two vectors can be found using
the angle between the two vectors can be found using
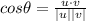
where
 is the scalar product between u and v
is the scalar product between u and v
 is the magnitude of u
is the magnitude of u
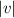 is the magnitude of v
is the magnitude of v
Here the two vectors that we have are:
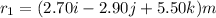
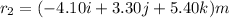
Their magnitudes are:
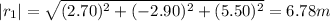
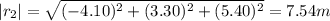
The scalar product is:
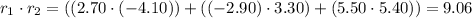
Therefore, the angle is: