Percent of red lights last between 2.5 and 3.5 minutes is 95.44% .
Explanation:
Step 1: Sketch the curve.
The probability that 2.5<X<3.5 is equal to the blue area under the curve.
Step 2:
Since μ=3 and σ=0.25 we have:
P ( 2.5 < X < 3.5 ) =P ( 2.5−3 < X−μ < 3.5−3 )
⇒ P ( (2.5−3)/0.25 < (X−μ)/σ < (3.5−3)/0.25)
Since, Z = (x−μ)/σ , (2.5−3)/0.25 = −2 and (3.5−3)/0.25 = 2 we have:
P ( 2.5<X<3.5 )=P ( −2<Z<2 )
Step 3: Use the standard normal table to conclude that:
P ( −2<Z<2 )=0.9544
Percent of red lights last between 2.5 and 3.5 minutes is
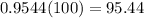 % .
% .