Question

a cylindrical cantilever beam is subjected to a perpendicular force with a magnitude of 300 Nat the tip. The beam rotates with a rotational speed of 2800 rpm. Determine how long it would take (in minutes) for the beam the fracture at the point where it's the most susceptable to failure. Neglet shear's effect on the fatigue, gravity, and the friction between the beam and the force

Answer 1

Here is the full question:

a cylindrical cantilever beam is subjected to a perpendicular force with a magnitude of 300 Nat the tip. The beam rotates with a rotational speed of 2800 rpm. Determine how long it would take (in minutes) for the beam the fracture at the point where it's the most susceptable to failure. Neglet shear's effect on the fatigue, gravity, and the friction between the beam and the force

Material Aluminium

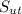`S_(ut)`(MPA) 280

L(cm) 150

r(cm) 2

Surface - Ground

Finish

Temperature Room

Reliability 99.9%

Answer:

1891.4399 minutes

Step-by-step explanation:

Given that:

The shaft is under rotational condition and Aluminum
`S_(ut) = \sigma_(ut) = 280 MPa`

L = 150 cm = 1500 mm

D = 2r = 2 × (2cm) = 4 cm = 40 mm

`\sigma_e = 0.4 \sigma_(ut)`

= 0.4 × 280 MPa

= 112 MPa

From here ; we start out by finding the revised endurance strength

`\sigma_e = \sigma_e *K_(surface finish)*K_(temp)*K_(relaiility)`

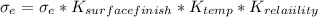
where;

`K_(surface finish) = a(S_(ut))^b`

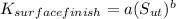
For ground condition; a = 1.58 ; b = - 0.085

`K_(surface finish) = 1.58*(280)^(-0.085)`

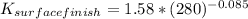
= 0.9786

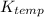`K_(temp)` = 1 for T < 300° C

`K_(reliability)` = 0.814 for 99.9% reliability

`\sigma_e = \sigma_e *K_(surface finish)*K_(temp)*K_(relaiility)`

`\sigma_e = 112*0.9786*1*0.814`

`\sigma_e =89.22 MPa`

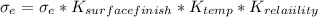
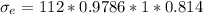
With the help of S-N diagram that is shown in the attached file below; we find the number of cycles before the fracture

From there; we determine the maximum bending stress in the shaft

`\sigma_b = (M\gamma)/(I) = (P*L*(d/2))/((\pi)/(64)d^4)`

`= (300*1500*((40)/(2)))/((\pi)/(64)40^4)`

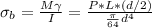
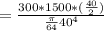
= 71.619 MPa

The Coordinates of the S-N diagram are as follows;

For Coordinates A; we have: (3, 2.4166)

For Coordinates B; we have: (6, 1.964)

For Coordinates C; we have : ( log₁₀ 71.619, log ₁₀ N)

Finally, using line equation

`y_2-y_1 = (y_2-y_1)/(x_2-x_1)(x-x_1)`

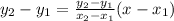
log ₁₀ S - 2.1466 = ( 1.964 - 2.4166)( log ₁₀ N - 3)

log ₁₀ 71.619 - 2.4166 = (-0.1508)( log ₁₀ N -3)

0.5615 = (-0.1508)( log ₁₀ N -3)

N = 5296031.731 revolutions

Thus, the shaft completes 5296031.731 revolutions before the fracture takes place.

To determine how long the time taken for fracture to occur; we have:

t =
`(5296031.731)/(2800)`

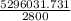
t = 1891.4399 minutes