Answer:
62.17% probability that a randomly selected exam will require more than 15 minutes to grade
Explanation:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this problem, we have that:
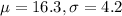
What is the probability that a randomly selected exam will require more than 15 minutes to grade
This is 1 subtracted by the pvalue of Z when X = 15. So

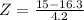

 has a pvalue of 0.3783.
has a pvalue of 0.3783.
1 - 0.3783 = 0.6217
62.17% probability that a randomly selected exam will require more than 15 minutes to grade