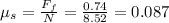a) 8.52 kN
b) 0.74 kN
c) 0.087
Step-by-step explanation:
a)
There are 3 forces acting on the car on the banked curve:
- The weight of the car,
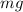 , vertically downward
, vertically downward
- The normal force of the pavement on the tires, N, upward perpendicular to the road
- The force of friction,
 , down along the road
, down along the road
Resolving the 3 forces along two perpendicular directions (horizontal and vertical), we obtain the equations of motions:
x- direction:
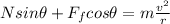 (1)
(1)
y- direction:
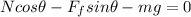 (2)
(2)
where
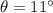 is the angle of the ramp
is the angle of the ramp
 is the force of friction
is the force of friction
m = 838 kg is the mass of the car
r = 151 m is the radius of the curve
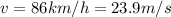 is the speed of the car
is the speed of the car
Solving eq.(2) for Ff and substituting into eq.(1), we can find the normal force:
From (2):
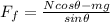 (3)
(3)
Substituting into (1) and re-arranging,
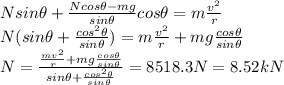
b)
The frictional force between the pavement and the tires,
 , can be found by using eq.(3) derived in part a):
, can be found by using eq.(3) derived in part a):
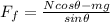
where we have:
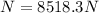 is the normal force
is the normal force
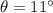 is the angle of the ramp
is the angle of the ramp
m = 838 kg is the mass of the car
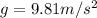 is the acceleration due to gravity
is the acceleration due to gravity
Substituting the values, we find:
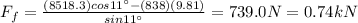
c)
The force of friction between the road and the tires can be rewritten as
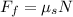
where
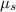 is the coefficient of static friction
is the coefficient of static friction
N is the normal force exerted by the road on the car
In this problem, we know that
N = 8.52 kN is the normal force
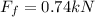 is the frictional force
is the frictional force
Therefore, the minimum coefficient of static friction between the pavement and the tires is: