Answer:
Maximum at points (8,0),(-8,0).Minimum at points (0,8), (0,-8).
Explanation:
There are multiple ways of using lagrange multipliers. Most of them are equivalent.
Consider the function
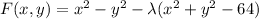 . We want the following
. We want the following
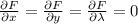 .
.
Then, we have
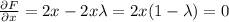
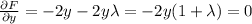
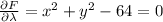
From the first two equations, we can see that if
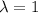 then necessarily y=0. IN that case, from the third equation (which is the restriction) gives us that
then necessarily y=0. IN that case, from the third equation (which is the restriction) gives us that
 .
.
On the other hand, if
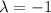 then necessarily x=0. Again, using the restriction this gives us that
then necessarily x=0. Again, using the restriction this gives us that
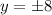 .
.
if we evaluate the original function in this points, we have that
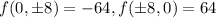 . Then, we have Maximum at points (8,0),(-8,0) and Minimum at points (0,8), (0,-8).
. Then, we have Maximum at points (8,0),(-8,0) and Minimum at points (0,8), (0,-8).