Differentiation of
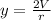 with respect to r is
with respect to r is
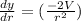 .
.
Explanation:
We have the following equation:
y=2V/r or
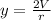 , we need to differentiate y with respect r , We know a formula of Differentiation that
, we need to differentiate y with respect r , We know a formula of Differentiation that

 i.e. differentiation of
i.e. differentiation of
 is
is
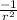 .
.
Now , let's solve this :
⇒
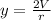
⇒
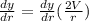
⇒

⇒

⇒
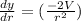
∴ Differentiation of
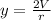 with respect to r is
with respect to r is
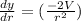 .
.