Question

Question 2 of 5

Marcos has a square sprocket ABCDgraphed in the coordinate plane. The square sprocket was rotated 180° about the origin to form
A'B'C'D'. The vertices are A'(-6, -3), B'(-2, -3), C (-2,1), and D'(-6,1). What are the coordinates of A?​

Answer 1

The coordinates of the point A is (6,3)

Step-by-step explanation:

Given that the Marcos has a square sprout ABCD graphed in the coordinate plane.

The square sprocket was rotated 180° about the origin to form A'B'C'D'.

The vertices are A'(-6, -3), B'(-2, -3), C (-2,1), and D'(-6,1).

We need to determine the coordinates of the point A.

Since, the rotation was 180° about the origin, the coordinate rule is given by

`(x,y)\implies(-x,-y)`

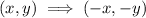
Using the above rule, let us translate the coordinate (-6, -3)

Substituting the value x = -6 and y = -3 in the coordinate rule, we get,

`(-6,-3)\implies(-(-6),-(-3))`

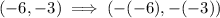
Simplifying, we get,

`(-6,-3)\implies(6,3)`

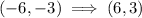
Thus, the coordinates of the point A is (6,3)