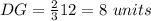Answer:
Part 1)
a)
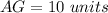
b)
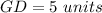
c)

d)

e)
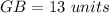
Part 2)
a)

b)

c)
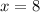
Part 3)
a) The height of the truss is 12 units
b) The centroid of triangle DEF is 8 units down from D
Explanation:
Part 1)
we know that
A centroid of a triangle is the point where the three medians of the triangle meet. A median of a triangle is a line segment from one vertex to the mid point on the opposite side of the triangle
The centroid divides each median in a ratio of 2:1
Part a) Find the length of the segment AG
we know that
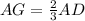 ---> the centroid divides each median in a ratio of 2:1
---> the centroid divides each median in a ratio of 2:1
we have
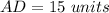
substitute
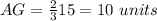
Part b) Find the length of the segment GD
we know that
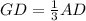 ---> the centroid divides each median in a ratio of 2:1
---> the centroid divides each median in a ratio of 2:1
we have
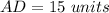
substitute

Part c) Find the length of the segment CD
we know that
In the right triangle CGD
Applying the Pythagorean Theorem
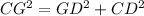
we have
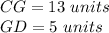
substitute
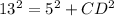
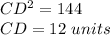
Part d) Find the length of the segment GE
we know that
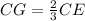 ---> the centroid divides each median in a ratio of 2:1
---> the centroid divides each median in a ratio of 2:1
we have
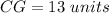
substitute
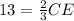

Find the length of the segment GE
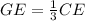
substitute
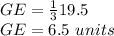
Part e) Find the length of the segment GB
we know that
In the right triangle GBD
Applying the Pythagorean Theorem
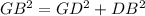
we have
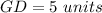
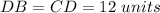 ---> D is the midpoint segment CB
---> D is the midpoint segment CB
substitute
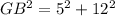
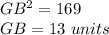
Part 2) Point L is the centroid of triangle NOM
Find the value of x
Part a) we have
OL=8x and OQ=9x+6
we know that
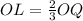 ---> the centroid divides each median in a ratio of 2:1
---> the centroid divides each median in a ratio of 2:1
substitute the given values
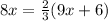
solve for x
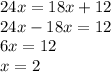
Part b) we have
NL=x+4 and NP=3x+3
we know that
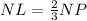 ---> the centroid divides each median in a ratio of 2:1
---> the centroid divides each median in a ratio of 2:1
substitute the given values
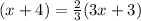
solve for x
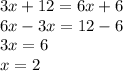
Part c) we have
ML=10x-4 and MR=12x+18
we know that
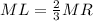 ---> the centroid divides each median in a ratio of 2:1
---> the centroid divides each median in a ratio of 2:1
substitute the given values
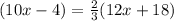
solve for x
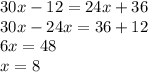
Part 3)
Part a) Find the altitude of the truss
Let
M ----> the midpoint of segment FE
DM ---> the altitude of the truss
Applying Pythagorean Theorem in the right triangle FDM
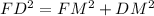
substitute the given values
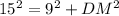
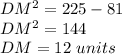
therefore
The height of the truss is 12 units
Part b) How far down from D is the centroid of triangle DEF?
we know that
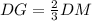 --> the centroid divides each median in a ratio of 2:1
--> the centroid divides each median in a ratio of 2:1
substitute the value of DM