Question

Segments CD, AE, and BF are medians of triangle ABC.

What is the value of x?

A. x = 1.9
B. x = 2.7
C. x = 5.5
D. x = 11

Answer 1

Option C: x = 5.5 is the value of x

Step-by-step explanation:

Given that CD, AE, an BF are the medians of the triangle ABC

Also, given that
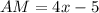`AM = 4x - 5` and
`ME=x+3`

We need to determine the value of x.

Since, we know that the centroid divides the median in the ratio 2 : 1

Hence, we have,

`AM=2* ME`

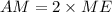
Substituting the values, we get,

`4x-5=2(x+3)`

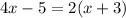
Simplifying, we get,

`4x-5=2x+6`

Subtracting both sides of the equation by 2x, we have,

`2x-5=6`

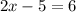
Adding both sides of the equation by 5, we have,

`2x=11`

Dividing both sides of the equation by 2, we get,

`x=5.5`

Therefore, the value of x is 5.5

Hence, Option C is the correct answer.