Answer:
 .
.
Explanation:
Since we are in quadrant two, cosine value is negative while sine value is positive.
We are going to use the Pythagorean Identity:
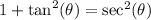 .
.
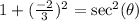

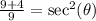
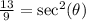
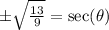
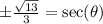
Since cosine and secant are reciprocals then they will have the same sign as along as they both exist.
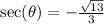
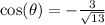 .
.
I don't see this answer as I'm going to rationalize the denominator.
 .
.
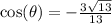 .
.