Question

Pls i literally do not know how to do this

Answer 1

• r = (n+1)/4
• the series diverges

Explanation:

The ratio test asks you to look at the ratio of two successive terms of the sum. It is generally convenient to look at the ratio ...

`(a_(n+1))/(a_n)`

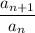
where
`a_n` is the term shown in parentheses to the right of the summation symbol. Here, that ratio is ...

`(\left((2(n+1)!)/(2^(2(n+1)))\right))/(\left((2n!)/(2^(2n))\right))=(2(n+1)!\cdot 2^(2n))/(2n!\cdot 2^(2(n+1)))\\\\=(2(n+1)!)/(2n!)\cdot(2^(2n))/(2^(2(n+1)))=(n+1)/((2^2)) = (n+1)/(4)`

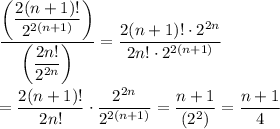
Most of the terms of the factorial product cancel, and the powers of 2 all cancel except for 2^2. So, the ratio of adjacent terms is ...

`\boxed{r_n=(n+1)/(4)}`

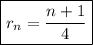
This gets larger and larger as n gets larger, so the series diverges.